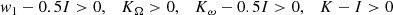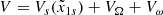| Issue |
Security and Safety
Volume 2, 2023
Security and Safety in Unmanned Systems
|
|
|---|---|---|
| Article Number | 2023020 | |
| Number of page(s) | 17 | |
| Section | Other Fields | |
| DOI | https://doi.org/10.1051/sands/2023020 | |
| Published online | 23 August 2023 | |
Research Article
Safety flight envelope calculation and protection control of UAV based on disturbance observer
College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 211106, China
* Corresponding authors (email: chenmou@nuaa.edu.cn)
Received:
23
March
2023
Revised:
13
June
2023
Accepted:
28
June
2023
In this paper, as for the unmanned air vehicle (UAV) under external disturbance, an attainable-equilibrium-set-based safety fight envelope (SFE) calculation method is proposed, based on which a prescribed performance protection control scheme is presented. Firstly, the existing definition of the SFE based on attainable equilibrium set (AES) is extended to make it consistent and suitable for the UAV system under disturbance. Secondly, a higher-order disturbance observer (HODO) is developed to estimate the disturbances and the disturbance estimation is applied in the computation of the SFE. Thirdly, by using the calculated SFE, a desired safety trajectory based on the time-varying safety margin function and first-order filter is developed to prevent the states of the UAV system from exceeding the SFE. Moreover, an SFE protection controller is proposed by combining the desired safety trajectory, backstepping method, HODO design, and prescribed performance (PP) control technique. In particular, the closed-loop system is established on the basis of disturbance estimation error, filter error, and tracking error. Finally, the stability of the closed-loop system is verified by the Lyapunov stability theory, and the simulations are presented to illustrate the effectiveness of the proposed control scheme.
Key words: Unmanned aerial vehicle (UAV) / safety flight envelope (SFE) / attainable equilibrium set (AES) / higher order disturbance observer (HODO) / backstepping method / prescribed performance control
Citation: Ma B and Chen M. Safety flight envelope calculation and protection control of UAV based on disturbance observer. Security and Safety 2023; 2: 2023020. https://doi.org/10.1051/sands/2023020
© The Author(s) 2023. Published by EDP Sciences and China Science Publishing & Media Ltd.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The unmanned air vehicle (UAV) represents a new type of aircraft weapon system that can be autonomously controlled and perform air-to-air and air-to-ground military missions [1]. Using UAVs to perform dangerous missions instead of pilot-piloted aircraft is one of the essential trends in future warfare [2]. Meanwhile, due to the advantages of UAVs, a large number of higher requirements have been proposed for the future applications of UAVs, such as intelligence, autonomy, large overload, and long-range, which can further promote the developments of UAVs.
Together with the wide applications of UAVs, flight safety issues have attracted much research attention from many scholars [3–6]. Normally, flight safety refers to the fact that during the operations of the aircraft, there are no incidents of improper operations or external factors (such as disturbances) that cause casualties or damage to the aircraft [7]. Compared with other traffic modes, the accident rate of aviation is low, while its destructiveness is enormous. Based on the results in [8], the leading cause of flight accidents was loss of control (LOC). Unfortunately, there is still no unified concept of the LOC far, and the causes of LOC are unclear [9]. However, it is widely recognized that the flight states exceeding the specific SFE can be considered LOC [10]. Though the LOC does not necessarily induce flight accidents, the accidents must occur sometime if it is undetected or left unchecked [11]. On the other hand, since UAVs are complex nonlinear systems and sensitive to disturbances, it is straightforward to cross the SFE during maneuvering and lead to LOC. Thus, designing SFE protection control systems is vital to prevent the LOC and ensure flight safety. Because of the great potential of the SFE protection system in enhancing flight safety, it has received extensive attention from researchers over two past decades [12]. Current researches on SFE protection systems mainly focus on two main fields: SFE computation and SFE-based controller design [13]. The former uses neural networks, dynamic trim, and reachability set to calculate the SFE, while the latter uses dynamic inverse, robust control, and intelligent control to prevent flight states from exceeding the SFE.
The premise of designing the SFE protection control system aims to obtain the SFE. The traditional SFE refers to the speed and altitude level flight envelope. However, even if the aircraft remains within this flight envelope, the outside disturbances will still induce the LOC problem, so a new concept of the SFE or an extended one need to be presented. It is widely accepted that the SFE comprises an environmental envelope, a structural envelope, and a dynamic envelope. The determination of dynamic envelope has caught many research interests since it takes the aircraft’s dynamic characteristics into account [14, 15]. Reference [16] completed the quantitative analysis of the LOC problem and determined the LOC quantitative criterion, which was composed of five different SFEs derived from the critical factors, such as aircraft’s dynamic characteristics, aerodynamic characteristics, structural integrity, and control variables. The LOC quantification criterion held that if the flight states exceed any three of the five envelopes, it can determine the LOC phenomenon that occurred. In addition, AES-based SFE was widely used in the field of flight safety [17, 18]. In [17], a calculation method of the SFE based on the AES was proposed to analyze the performance and maneuverability of aircraft in steady flight conditions, involving the calculation of two-dimensional AESs for various aircraft and subsequent analysis of maneuvering characteristics. In [18], the AES of a UAV was determined using the discrete-time Newton iteration approach, and a prediction technique for AES was developed in conjunction with the Unscented Kalman Filter, providing the benefits of high accuracy and exceptional stability. Currently, the calculation of the AES-based SFE is mainly built on the nominal systems, that is, some unfavorable factors such as disturbance and model uncertainties are not involved, which remains challenging and important. Especially, in actual flight, the UAVs are unavoidably affected by various outside disturbances, which means that an extension of the AES concept waits to be proposed.
Once the SFE is obtained, the SFE protection control system needs to be established. For nominal systems, some research results have emerged on the SFE protection control. In [7], an L1 adaptive control scheme was proposed and implemented in a flight envelope protection system for a transport-class aircraft, which enhanced aircraft performance by restoring the nominal performance of the baseline controller under faults and disturbances. An SFE protection system was developed in [19], and it was based on command-limiting architecture, which could enhance the standard gain-scheduling control law by considering the LOC quantitative criterion. A safety control scheme integrating SFE protection and reference command regeneration was proposed in [20] to address the issue of performance degradation and SFE shrinkage resulting from aircraft actuator faults, which involved the calculation of AES-based SFE and a sliding mode control scheme incorporating prescribed performance functions. In [21], an effective convex optimization-based algorithm was developed to solve AES by representing it as a half-space, and a protection control law based on model predictive control was developed by incorporating the AES constraints. In [22], a sparse recurrent fuzzy neural network was utilized to propose an SFE protection system, where a fault-tolerant controller served as the baseline controller to handle model uncertainties and a dynamic SFE protection controller was implemented to prevent the compromised aircraft from breaching the SFE. A command-limiting SFE protection system was developed in [23] and incorporated an exponential potential function defined based on the SFE, where the controller design utilized the gradient of the exponential potential function. To enhance aircraft safety, an SFE protection system was developed in [24], where the SFE protection algorithm was designed by incorporating an adaptive neural network, the least square method, and an online linearization algorithm to predict the states based on the current control inputs and states. In [25], an online SFE protection system including system identification, damage classification, flight-envelope prediction, and fault-tolerant control was proposed for impaired aircraft, and with the designed envelope protection, the LOC accidents were more likely to be prevented. However, as for the application of SFE protection control, it is not enough to only consider these ideal situations. In practice, the SFE is always affected by various factors, such as outside disturbances. Then, for a class of uncertain nonlinear systems with output constraints and external disturbances, an adaptive neural safety boundary protection algorithm was developed in [26] based on disturbance observer, which could effectively limit the output trajectory within the output constraints, ensuring flight safety. For unmanned helicopters under outside disturbances, model uncertainties, and output constraints, an adaptive fuzzy safety tracking control scheme was developed [27], where the safety margin was used to limit the desired output within a given range, and a tracking protection controller was designed by combining a fuzzy system. In summary, the existence of the disturbance will impose negative effects on the SFE of the UAV system, and deteriorate the performance of the SFE protection controller, which needs to be investigated and constitutes the focus of this paper.
Motivated by the above discussions on SFE computation and SFE-based protection control, this paper proposes a co-design of a disturbance-observer-based AES calculation method and an SFE protection control scheme. The main contributions of this paper are listed as follows:
-
The scope of the applications of existent AES is extended, and the definition of the AES-based SFE under disturbances is presented. That is to say, a HODO is developed to estimate external disturbances, and the disturbance observations are used for the calculation of the SFE;
-
Based on the derived SFE, a time-varying safety margin function is proposed based on the prescribed performance function and safety margin constant. Then, by utilizing the safety margin function, a co-design method for the desired safety trajectory and SFE protection controller is proposed.
Five sections make up the whole structure of this paper. In Section 2, the UAV attitude motion model is given. The definition and computation of AES under disturbance are studied based on the HODO in Section 3. Section 4 proposes a method for generating the safety desired trajectory. Also, an SFE protection control law is developed in Section 4 based on the HODO, backstepping method, and PP control. Section 5 designs and completes simulations to verify the effectiveness of the SFE protection controller. The entire work is summarized in Section 6.
2. Problem statement
This section gives the UAV attitude dynamic model under external disturbances, the control targets, and some related preliminary knowledge. Initially, the disturbances are taken into account in the fast-loop of the UAV’s attitude dynamics, which is given as follows [28]:
where x1 = [α, β, μ]T ∈ ℝ3 denotes the attitude angle vector including the attack angle, sideslip angle, and roll angle, x2 = [p, q, r]T ∈ ℝ3 represents the attitude angle rate vector of roll angle rate, pitch angle rate, and yaw angle rate, ![$ \bar{x}_2=\left[x_1^{\mathrm{T}}, x_2^{\mathrm{T}}\right]^{\mathrm{T}} \in \mathbb{R}^6 $](/articles/sands/full_html/2023/01/sands20230008/sands20230008-eq2.gif) , u = [δa,δc,δr,δy,δz]T ∈ ℝ5 is the control input vector that, respectively, represents the aileron, canard, rudder, lateral thrust vectoring, and normal thrust vectoring deflection angles; f1 : ℝ3 → ℝ3 and f2 : ℝ6 → ℝ3 are the nonlinear vector-valued functions, g1 : ℝ3 → ℝ3 × 3 and g2 : ℝ6 → ℝ3 × 5 are the nonlinear matrix-valued functions. The expressions of f1, g1, f2, g2 can be found in [29]. Here, d(t)=[dp(t),dq(t),dr(t)]T ∈ ℝ3 means the external time-varying disturbance, and y ∈ ℝ3 denotes the output vector.
, u = [δa,δc,δr,δy,δz]T ∈ ℝ5 is the control input vector that, respectively, represents the aileron, canard, rudder, lateral thrust vectoring, and normal thrust vectoring deflection angles; f1 : ℝ3 → ℝ3 and f2 : ℝ6 → ℝ3 are the nonlinear vector-valued functions, g1 : ℝ3 → ℝ3 × 3 and g2 : ℝ6 → ℝ3 × 5 are the nonlinear matrix-valued functions. The expressions of f1, g1, f2, g2 can be found in [29]. Here, d(t)=[dp(t),dq(t),dr(t)]T ∈ ℝ3 means the external time-varying disturbance, and y ∈ ℝ3 denotes the output vector.
The control objective of this paper is to design a HODO-based SFE protection controller to keep the state x1 of the system (1) within the SFE constraint. For this reason, the calculation of AES under disturbance is initially studied. Then, a method of obtaining the safety desired trajectory from the desired trajectory is proposed by combining the time-varying safety margin function and the first-order filter. Finally, SFE protection control controller is designed based on the backstepping method, the HODO, and the PP control.
The following assumptions and lemma are given to facilitate the subsequent calculation of the SFE and the design of the SFE protection control scheme.
[27] The desired trajectory yd = x1d = [αd, βd, μd]T with its first and second derivatives, 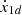 and
and 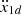 , are all bounded for t ≥ 0. That is, there exists a constant M > 0 such that
, are all bounded for t ≥ 0. That is, there exists a constant M > 0 such that
[30]. The unknown external time-varying disturbance d(t) and its first rth derivatives are all bounded for t ≥ 0, that is, ∥d(j)∥2 ≤ ηj, where ηj > 0, j ∈ {0, 1, …, r} are unknown constants.
Assumptions 1 and 2 are the standard assumptions that have been widely adopted in many publications such as [26, 27], [30], and [31]. Here, Assumption 1 implies that the desired trajectory yd is of finite energy. For Assumption 2, the disturbance d(t) is assumed to be smooth and bounded while its bounds are unknown, which is crucial for the design of the disturbance observer.
For a control system with the bounded initial condition, if there exists a C 1 continuous and positive definite Lyapunov function V(x): ℝ n → ℝ such that
where ϑ1, ϑ2 : ℝ → ℝ are class K functions, κ1 > 0, and κ2 > 0, then the state x(t) is uniformly bounded [27].
3. Safety flight envelope calculation under disturbance
According to the basic concept of dynamic trim, the UAV system with twelve states can be divided into four loops: the position loop, the velocity loop, the attitude angle loop, and the attitude angle rate loop. The attitude angle loop and the attitude angle rate loop belong to the fast loop, while the position loop and the speed loop belong to the slow loop. In the UAV system, the states of the fast loop first reach the equilibrium point. That is to say, the derivatives of the fast states are normally zero, while the slow states remain constants. The AES represents the set of all dynamic trim points of the UAV and is defined as the SFE of the UAV. As an extension of the AES definition, this section introduces a new type of AES under disturbance and gives its computation method.
Considering the system (1) without the disturbance d(t), the dynamic model is rewritten as
The deflections of the rudders of the UAV system are limited within a specific range, which can generally be obtained as
where δi, max, δi, min represent the upper bound and lower bound of δi, i ∈ {a, c, r, y, z}, respectively. Then, considering the definition of AES in [17], the AES of system (5) can be written as
where S ⊂ ℝ6 denotes the AES. Once the parameters of system (5) are given, S is uniquely determined and does not change with time on.
Considering equation (1), it can be seen that the outside disturbance will change the dynamic trim points of the UAV system. Then, a trim point without the disturbance may become an untrimmed point, which means that considering the problem of the AES under disturbance is essential and challenging.
Due to the introduction of external disturbance, the AES in (7) will become altered and unpredictable. By combining the idea of dynamic trim and the definition of AES, we define a time-varying AES of equation (1) as:
where Sd(t)⊂ℝ6 denotes the AES under disturbance. It is worth noting that even though the AES in (8) has its rationality and application value, equation (8) contains a time-varying disturbance, usually unknown, which makes the AES uncomputable.
Considering that in the control law design and the SFE computation, a technique of estimating the disturbance needs to the proposed to observe the time-varying unknown disturbance. Therefore, for the convenience of calculation, the observed value 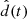 of the disturbance d(t) is used to replace the d(t) described in equation (8).
of the disturbance d(t) is used to replace the d(t) described in equation (8).
The approximate set  of the AES Sd(t) under disturbance can be further extended as:
of the AES Sd(t) under disturbance can be further extended as:
In order to obtain the estimation of the disturbance, the following HODO is introduced [30]
where zm ∈ ℝ3, m ∈ {1, 2, …, r} are the internal states of the HODO and  are the estimated values of
are the estimated values of  , respectively;
, respectively;  is the output of the HODO, km ∈ ℝ3 × 3, m ∈ {1, 2, …, r} are positive definite matrices to be designed. In what follows, define the qth order derivative estimation error
is the output of the HODO, km ∈ ℝ3 × 3, m ∈ {1, 2, …, r} are positive definite matrices to be designed. In what follows, define the qth order derivative estimation error  of the disturbance d as:
of the disturbance d as:
where q ∈ {0, 1, …, r − 1} and  . Taking the derivative of
. Taking the derivative of  and invoking equations (1) and (10), one can obtain
and invoking equations (1) and (10), one can obtain
Denoting ![$ \tilde{D}=\left[\tilde{d}^{\mathrm{T}},\tilde{\dot{d}}^{\mathrm{T}}, \ldots,(\tilde{d}^{(r-1)})^{\mathrm{T}}\right]^{\mathrm{T}} \in \mathbb{R}^{3 r} $](/articles/sands/full_html/2023/01/sands20230008/sands20230008-eq23.gif) , then the error dynamic in equation (12) can be rewritten in a compact form as
, then the error dynamic in equation (12) can be rewritten in a compact form as
where
Constructing the Lyapunov function  for equation (13), taking the derivative of
for equation (13), taking the derivative of  , and applying Young’s inequality, one yields
, and applying Young’s inequality, one yields
where I is the identity matrix with the appropriate dimension. From Assumption 2, the following inequality is established
Considering equations (17) and (16) can be rewritten as
If the parameter K to be designed satisfies K − 0.5I > 0, then according to equation (18) and Lemma 1, the estimated error  of the HODO is uniformly bounded.
of the HODO is uniformly bounded.
The basic idea of the AES under disturbance aims to estimate the disturbance online and replace the disturbance with its observed values to calculate AES. In practical applications, due to the limitation of the computing power of the flight control computer, it can be considered to store offline AES under disturbances. When flying online, according to the observed value of the disturbance, the AES can be generated from the stored AES through interpolation. In this paper, we only consider the offline computation of the AES under external disturbance. Thus, based on the optimization method, the calculation of the AES with disturbance can be transformed into an optimization problem, which is described as [20]
where S1 ∈ ℝ3 × 3 and S2 ∈ ℝ3 × 3 are positive definite matrices to be predefined. J : ℝ6 → ℝ is the objective function.
From (9), the optimization problem (19) has simple constraints, and its objective function is continuously differentiable. Thus, some first-order or second-order methods, such as the gradient, Newton, and Trust Region, can be utilized to solve such problems (19) since they are all based on iteration. The iterative procedure means that it starts from an initial point, looks for the next point that reduces the objective function, until the termination condition is satisfied, then the algorithm stops.
4. PP-based flight envelope protection control scheme
Since flight safety is the first issue for UAVs, it is essential for the flight control law to conduct maneuvering flights and complete specified tasks, which needs SFE protection control to realize flight safety. Then, for the attitude dynamic model of the UAV system under disturbance, this section proposes a new SFE control method by integrating the HODO, the calculation of SFE, the filtering technology, and the prescribed performance control. The SFE protection control involves both the SFE constraints and the performance requirements of tracking control, such as steady-state and transient performances.
Since the SFE of the system (1) is altered due to time-varying disturbance, there must exist the SFE constraint upper bound xu p(t)=[αu p(t),βu p(t),μu p(t)]T and SFE constraint lower bound xl o w(t)=[αl o w(t),βl o w(t),μl o w(t)]T such that αu p(t)> αl o w(t), βu p(t)> βl o w(t), and μu p(t)> μl o w(t). Yet, the conflicts between desired trajectory x1d = [αd, βd, μd]T and SFE constraints may occur in actual flight. Then, it is necessary to adjust the desired trajectory x1d to obtain the constraint desired trajectory x1c = [αc, βc, μc]T and the safety desired trajectory x1s = [αs, βs, μs]T to ensure flight safety.
This section proposes a new generation method of constraint and desired safety trajectories based on the PP functions. The procedure is mainly divided into three following steps [27]:
Step 1: The first step is to obtain the SFE constraints xup(t) and xlow(t). According to the calculation of the SFE proposed in the previous section, xup(ti), xlow(ti), i ∈ {1, 2, …, n} at a given moment can be obtained. Piecewise Hermit interpolation functions xup(t) and xlow(t) can be constructed by using xup(ti), xlow(ti), i ∈ {1, 2, …, n}. Both xup(t) and xlow(t) are piecewise continuously differentiable.
Step 2: The second step is to generate the desired constraint trajectory x1c. Let ρα(t), ρβ(t), and ρμ(t) be the performance functions of the angle-of-attack tracking error eα = α − αs, sideslip angle tracking error eβ = β − βs, and roll angle tracking error eμ = μ − μs, respectively. It is necessary to design the SFE protection control law such that the errors ei, i ∈ {α, β, μ} satisfy [32]
where 0 < δi < 1, i ∈ {α, β, μ} are the parameters to be designed. Here, ρi(t), i ∈ {α, β, μ} are selected as [32]
where ρi0 and ρi∞ denote the initial and limit values of performance functions with ρi0 > ρi∞ > 0, li > 0.
Define that τα, τβ, and τμ are the safety margin constants to be designed later. The time-varying safety margin functions are constructed as min{ρi(t),τi}, i ∈ {α, β, μ}. Figure 1 shows a schematic diagram of the time-varying safety margin functions. Moreover, the schematic diagram of generating the constrained desired trajectory according to the time-varying safety margin function, the desired trajectory, and the upper and lower bounds of the SFE are illustrated in Figure 2.
 |
Figure 1. The time-varying safety margin function changes over time |
 |
Figure 2. Constrained desired trajectory generation process |
Let’s take αc as an example to illustrate this analytic process. When αd(t)≥αup(t)−min{τα, ρα(t)}, the desired trajectory has the risk of crossing the upper bound of the SFE. Define the desired constraint trajectory as
As for αd(t)≤αlow(t)+min{τα, ρα(t)}, the desired trajectory has the risk of crossing the lower bound of the SFE. Define the constrained desired trajectory as
For αlow(t)+min{τα, ρα(t)} < αd(t)< αup(t)−min{τα, ρα(t)}, the desired trajectory has margins from the upper bound and lower bound of the SFE. The constrained desired trajectory is defined as
In summary, αc can be further written as
Similarly, βc and μc can be accordingly obtained as
Based on the above discussions, we can define the desired constraint trajectory x1c = [αc, βc, μc]T. Since min{ρi(t),τi}, i ∈ {α, β, μ}, xup(t), and xlow(t) are all piecewise continuously differentiable and bounded, then x1c is also a piecewise continuously differentiable bounded function. That is, in each differentiable interval, there must exist a constant Q > 0 such that
Step 3: The desired constraint trajectory defined in the above step is piecewise continuously differentiable, which is inconvenient for the subsequent tracking control law design. Then, a first-order filter is introduced for the smoothing, and it is designed as follows [33]
where x1s ∈ ℝ3 is the estimate of the constrained desired trajectory x1c, called the safety desired trajectory.  is a positive definite matrix that needs to be designed later.
is a positive definite matrix that needs to be designed later.
Defining the filter error  and taking the derivative of
and taking the derivative of  with respect to time, we have
with respect to time, we have
For equation (30), the Lyapunov function is selected as
Now, differentiating  with respect to time and invoking equation (30), one yields
with respect to time and invoking equation (30), one yields
Then, considering equations (28) and (32) can be rewritten as
One can check that if the parameter w1 to be designed satisfies w1 − 0.5I > 0, then according to equation (33) and Lemma 1, the filter error  is uniformly bounded.
is uniformly bounded.
Based on the safety-designed trajectory generated above, the control law is designed with the PP control method to make the output y = x1 of equation (1) track x1s in order to ensure flight safety. The attitude angle tracking error eΩ ∈ ℝ3 and attitude angle rate tracking error ew ∈ ℝ3 are defined as
where x2 * ∈ ℝ3 is the virtual control law to be designed. Taking the derivative of eΩ with respect to time and invoking equations (1), (35), one yields
Moreover, according to the error transformation in [32], the transformed error can be obtained as
where εi ∈ ℝ is the transformed error of the error variable ei, zi = ei(t)/ρi(t), i ∈ {α, β, μ}. Si : ℝ → ℝ are the error transformation functions and can be written as
Taking the derivative of εi with respect to time yields
where ri = (∂Si −1/∂zi)(1/ρi), i ∈ {α, β, μ}. Since both ∂Si −1/∂zi and ρi are greater than 0, ri > 0.
Defining R(t)=diag(rα,rβ,rμ),  , N(t)=[Nα(t),Nβ(t),Nμ(t)]T, i ∈ {α, β, μ}, equation (39) can be written in the compact form as
, N(t)=[Nα(t),Nβ(t),Nμ(t)]T, i ∈ {α, β, μ}, equation (39) can be written in the compact form as
where εΩ = [εα, εβ, εμ]T. By substituting equations (36) into (40), then  can be rewritten as
can be rewritten as
Thus, the virtual control law x2 * is designed as
where  is the positive definite matrix to be designed, that is,
is the positive definite matrix to be designed, that is,  . Substituting equations (42) into (41),
. Substituting equations (42) into (41),  can be obtained as
can be obtained as
For equations (43), the Lyapunov function VΩ is constructed as
Differentiating VΩ with respect to time and invoking equation (43) yield
Meanwhile, by considering equation (1), the derivative of ew can be obtained as
Then, the control law is designed as
where  is the positive definite matrix to be designed, that is,
is the positive definite matrix to be designed, that is,  . Thus, substituting equations (47) into (46) yields
. Thus, substituting equations (47) into (46) yields
For error dynamic (48), the Lyapunov function Vw is selected as
Taking the derivative of Vw with respect to time and invoking equation (18),  can be written as
can be written as
Motivated by the above discussions, as for the system (1), the stability analysis of the SFE protection control law designed based on the HODO and the backstepping method can be summarized as the following theorem.
For the nonlinear attitude control UAV system (1) under outside disturbance, Assumptions 1 and 2 are satisfied, the design of HODO is shown in (10), and the SFE under external disturbance is defined in (9) and computed by (19), the constrained desired trajectories are designed by (25), (26), and (27), based on which the safety desired trajectories are obtained by (29), and the design of virtual control law x2* and control input u are designed as (42) and (47). Then, as for the performance functions ρi(t),i = (α, β, μ) taken as (21) with 0 < δi < 1 and the safety margin constants τi > 0, the UAV attitude SFE protection tracking errors are bounded convergent, and the signals of all closed-loop systems are uniformly bounded if there exist positive definite matrices w1, KΩ, Kω, and K such that
In order to prove Theorem 1, the overall Lyapunov function V is constructed as
Taking the derivative of V with respect to time, invoking equations (33), (45), (50), and noticing the fact that  , we have
, we have
where ϖ = min{σmin(w1−0.5I),σmin(KΩ),σmin(Kω−0.5I),σmin(K2−I)} > 0, σmin(L) represents the smallest eigenvalue of matrix L, c0 = 0.5ηr 2 + 0.5Q. According to Lemma 1, the signals of the closed-loop systems are uniformly bounded, and the proof of Theorem 1 is completed.▫
5. Numerical simulations
In this section, simulations are presented to calculate AES under disturbance, based on which the effectiveness of the proposed SFE protection controller is verified.
Set the initial conditions for the simulation: flight altitude H(0)=3000 m, flight velocity V(0)=150 m/s, engine thrust T = 20, 000N, attitude angle α(0)=β(0)=μ(0)=5°, attitude angle rate p(0)=q(0)=r(0)=5 ° /s. In the simulation, the trust region algorithm is used to solve equation (19), and the parameters are selected as S1 = diag(3, 3, 3),S2 = diag(1, 1, 1). Moreover, the disturbance d(t) is assumed as d(t)=[0.25sin(t),0.3sin(1.5t),0.25sin(2t)]T. The desired trajectories are taken as:
By exploiting Theorem 1 and taking the order of HODO as 2, the gain matrices of the HODO are taken as k1 = diag(10, 10, 10), k2 = diag(3, 3, 3). The parameters of the prescribed performance functions are taken as: ρα0 = ρβ0 = ρμ0 = 0.2 rad, ρα∞ = ρβ∞ = ρμ∞ = 0.01 rad, lα = lβ = lμ = 1, δα = δβ = δμ = 0.8. The safety margin constants are τα = τβ = τμ = 0.05 rad. The parameter of the first-order filter is selected as w1 = diag(12.5, 12.5, 12.5). The controller gain matrices are taken as KΩ = Kω = diag(5, 5, 5). Based on Theorem 1, the selection of the designed parameters is mainly based on equation (51), and the parameters satisfying equation (51) can meet the desired control target. Moreover, the initial values of the internal states z1 and z2 of the HODO are taken as z1 = z2 = [0, 0, 0]T. The simulation is mainly from the SFE calculation and the requirements of the safety tracking accuracy to debug the parameters. Then, a series of parameter values are selected, and the optimal parameters are obtained according to the disturbance tracking error and SFE tracking accuracy.
Figure 3 shows the comparisons of the SFE under disturbance and the one without disturbance. It can be seen from Figure 3 that compared with the case without disturbance, the SFE under disturbance can shrink significantly, which means that when designing a boundary protection controller, the impact of disturbance should be taken into account. Otherwise, the performance loss of flight control may occur. The safety tracking curves of the attack, sideslip, and roll angles are illustrated in Figures 4–6. Figure 4 indicates that the attitude protection control law of this paper can achieve adequate protection against the angle of attack. The desired signal of the attack angle does not violate the lower bound of the safety boundary in the whole control process. However, it violates the upper bound of the safety boundary for many times. Due to the time-varying safety margin, when the reference signal of the attack angle is close to the upper bound of the SFE, the SFE protection control system makes corresponding modifications to the reference signal of the attack angle, which can ensure flight safety and avoid LOC. It follows from Figures 5 and 6 that the designed attitude protection control law can realize the protection of sideslip angle and roll angle. During the entire control process, the sideslip angle reference signal and the roll angle reference signal violate the upper and lower bounds of the SFE many times, and the protection control system successfully adjusts the signal to violate the boundary to ensure flight safety.
 |
Figure 3. Upper and lower bounds of SFE. (a) Upper and lower bounds of attack angle, (b) Upper and lower bounds of slide angle and (c) Upper and lower bounds of roll angle |
 |
Figure 4. The curve of attack angle during protection control |
 |
Figure 5. The curve of slideslip angle during protection control |
 |
Figure 6. The curve of roll angle during protection control |
The attitude angle tracking errors in the protection control process are shown in Figure 7. Figure 7 shows that the tracking errors are strictly limited in the upper and lower bounds composed of prescribed performance functions. With time on, the upper and lower bounds of the preset performance gradually decrease, the attitude angle tracking error converges, and the prescribed performance conditions are always satisfied. Moreover, we give detailed diagrams of attack angle SFE, desired trajectory, constraint desired trajectory, safety desired trajectory, and actual tracking trajectory in the protection control process, as shown in Figure 8. It can be seen from Figure 8 that the desired constraint trajectory, the safety desired trajectory, and the actual tracking trajectory are strictly limited within the SFE constraints, which ensures flight safety. Finally, each channel’s disturbance and estimated value are presented, as shown in Figure 9. Figure 9 indicates that the HODO designed in this paper can quickly and accurately estimate unknown time-varying disturbances.
 |
Figure 7. The tracking errors of attitude angles during simulation. (a) The tracking error of attack angle, (b) the tracking error of slideslip angle and (c) The tracking error of roll angle |
 |
Figure 8. Simulation details of attack angle during protection control |
 |
Figure 9. Disturbances and their estimations. (a) dp and |
6. Conclusions
In this paper, as for the attitude dynamic model of the UAV system under disturbance, the extension and calculation of the SFE based on HODO and AES were first investigated. Secondly, a time-varying safety margin function was constructed, and a desired safety trajectory generation method was proposed. Then, by combining the prescribed performance control, the HODO, and the backstepping method, a SFE protection controller was designed. Finally, simulation results showed that the SFE under disturbance could shrink obviously, and the SFE protection control scheme could achieve the protection of the attitude angles during tracking control. In this article, we mainly focused on the theory and the simulation rather than the experiment, which was mainly due to the lack of supporting conditions for doing the experiment. If possible in the future, we will make up for the experiment.
The main advantages of this paper are summarized in what follows. Firstly, the disturbances are considered in the computation of the SFE, and the influence of the disturbances on the SFE is analyzed. Secondly, a method for generating the safety desired trajectory is constructed based on the time-varying safety margin function and first-order filter, which guarantees that the desired trajectory remains within the SFE. Finally, an SFE protection controller is deduced by combining the HODO, prescribed performance control, and the backstepping method. In future studies, both model uncertainties and outside disturbance in the UAV system will be jointly considered. Moreover, the protection control inside the SFE with the one outside the SFE will need to be considered simultaneously to ensure flight safety in the case of state crossing caused by a sudden change of state.
Conflict of Interest
The author declares no conflict of interest.
Data Availability
No data are associated with this article.
Authors’ Contributions
Biao Ma contributed to the investigation, writing, and validation. Mou Chen contributed to the methodology, project administration, and conceptualization
Acknowledgments
Thanks to the anonymous reviewers for their helpful comments and suggestions.
Funding
This work was supported in part by the National Science Fund for Distinguished Young Scholars 61825302; in part by the National Natural Science Foundation of China under Grant U2013201 and in part by the Key R & D projects (Social Development) in Jiangsu Province of China under Grant BE2020704.
References
- Fahlstrom PG, Gleason TJ and Sadraey MH. Introduction to UAV Systems. John Wiley & Sons, 2022. [Google Scholar]
- Kim J, Kim S and Ju C et al. Unmanned aerial vehicles in agriculture: a review of perspective of platform, control, and applications. IEEE Access 2019; 7: 105100–15. [CrossRef] [Google Scholar]
- Tang L, Roemer M and Ge JH et al. Methodologies for adaptive flight envelope estimation and protection. In: AIAA Guidance, Navigation, and Control Conference. AIAA, 2009. [Google Scholar]
- Harno HG and Kim Y. Safe flight envelope estimation for rotorcraft: a reachability approach. In: 18th International Conference on Control, Automation and Systems (ICCAS). IEEE, 2018, 998–1002. [Google Scholar]
- van den Brandt R and de Visser CC. Safe flight envelope uncertainty quantification using probabilistic reachability analysis. IFAC-Pap 2018; 51: 628–35. [Google Scholar]
- Lu ZD, Hong HC and Gerdts M et al. Flight envelope prediction via optimal control-based reachability analysis. J Guid Control Dyn 2022; 45: 185–95. [CrossRef] [Google Scholar]
- Lee H, Snyder S and Hovakimyan N. L1 adaptive control within a flight envelope protection system. J Guid Control Dyn 2017; 40: 1013–26. [CrossRef] [Google Scholar]
- Belcastro C and Foster J. Aircraft loss-of-control accident analysis. In: AIAA Guidance, Navigation, and Control Conference. AIAA, 2010. [Google Scholar]
- Falkena W, Borst C and Chu QP et al. Investigation of practical flight envelope protection systems for small aircraft. J Guid Control Dyn 2011; 34: 976–988. [CrossRef] [Google Scholar]
- Nabi HN, Lombaerts T and Zhang Y et al. Effects of structural failure on the safe flight envelope of aircraft. J Guid Control Dyn 2018; 41: 1257–75. [CrossRef] [Google Scholar]
- Zhang Y, de Visser CC and Chu QP. Online safe flight envelope prediction for damaged aircraft: a database-driven approach, In: AIAA Modeling and Simulation Technologies Conference. AIAA, 2016. [Google Scholar]
- Lombaerts T, Schuet S and Acosta D et al. On-Line Safe Flight Envelope Determination for Impaired Aircraft. Springer, 2015. [Google Scholar]
- Cao YH, Wu ZL and Su Y et al. Aircraft flight characteristics in icing conditions. Prog Aerosp Sci 2015; 74: 62–80. [CrossRef] [Google Scholar]
- Stapel J, de Visser CC and Van Kampen EJ et al. Efficient methods for flight envelope estimation through reachability analysis. In: AIAA Guidance, Navigation, and Control Conference, AIAA, 2016. [Google Scholar]
- Helsen R, Van Kampen EJ and de Visser CC et al. Distance-fields-over-grids method for aircraft envelope determination, J Guid Control Dyn 2016; 39: 1470–80. [CrossRef] [Google Scholar]
- Wilborn J and Foster J. Defining commercial transport loss-of-control: a quantitative approach. In: AIAA Atmospheric Flight Mechanics Conference and Exhibit. AIAA, 2004. [Google Scholar]
- Goman MG, Khramtsovsky AV and Kolesnikov EN. Evaluation of aircraft performance and maneuverability by computation of attainable equilibrium sets. J Guid Control Dyn 2008; 31: 329–39. [CrossRef] [Google Scholar]
- Lu SM, Chen M and Li MS. Flight envelope predicting algorithm for uav based on UKF. In: 2019 Chinese Control Conference. IEEE, 2019, 3029–34. [Google Scholar]
- Tekles N, Chongvisal J and Xargay E et al. Design of a flight envelope protection system for NASA’s transport class model. J Guid Control Dyn 2017; 40: 863–77. [CrossRef] [Google Scholar]
- Yu X, Zhou XB and Zhang YM et al. Safety control design with flight envelope protection and reference command generation. IEEE Trans Aerosp Electron Syst 2022; 58: 5835–48. [CrossRef] [Google Scholar]
- Zogopoulos Papaliakos G and Kyriakopoulos KJ. A flight envelope determination and protection system for fixed-wing UAVs. In: IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2020, 9599–605. [CrossRef] [Google Scholar]
- Xie R, He HH and Meng XB et al. Neural-network-based dynamic flight envelop protection within integrated aircraft control system. J Guid Control Dyn 2023; 1–12, doi: 10.2514/1.G006872. [CrossRef] [Google Scholar]
- Sun DL, Hovakimyan N and Jafarnejad Sani H. Design of command limiting control law using exponential potential functions. J Guid Control Dyn 2020; 44: 1–8. [Google Scholar]
- Shin H and Kim Y. Flight envelope protection of aircraft using adaptive neural network and online linearisation. Int J Syst Sci 2016; 47: 868–85. [CrossRef] [Google Scholar]
- Zhang Y, Huang YZ and Chu QP et al. Database-driven safe flight-envelope protection for impaired aircraft. J Aerosp Inf Syst 2021; 18: 14–25. [Google Scholar]
- Chen M, Ma HX and Kang Y et al. Adaptive neural safe tracking control design for a class of uncertain nonlinear systems with output constraints and disturbances. IEEE Trans Cybern 2022; 52: 12571–82. [CrossRef] [PubMed] [Google Scholar]
- Ma HX, Chen M and Feng G et al. Disturbance-observer-based adaptive fuzzy tracking control for unmanned autonomous helicopter with flight boundary constraints. IEEE Trans Fuzzy Syst 2022; 31: 184–98. [Google Scholar]
- Chen M. Constrained control allocation for overactuated aircraft using a neurodynamic model. IEEE Trans Syst Man Cybern Syst 2015; 46: 1630–41. [Google Scholar]
- Snell SA. Nonlinear Dynamic-Inversion Flight Control of Supermaneuverable Aircraft. University of Minnesota, 1991. [Google Scholar]
- Yan XH, Chen M and Feng G et al. Fuzzy robust constrained control for nonlinear systems with input saturation and external disturbances. IEEE Trans Fuzzy Syst 2019; 29: 345–56. [Google Scholar]
- Xian B, Guo JC and Zhang Y. Adaptive backstepping tracking control of a 6-DOF unmanned helicopter. IEEE/CAA J Autom Sin 2015; 2: 19–24. [CrossRef] [Google Scholar]
- Bechlioulis CP and Rovithakis GA. Robust adaptive control of feedback linearizable mimo nonlinear systems with prescribed performance. IEEE Trans Autom Control 2008; 53: 2090–9. [CrossRef] [Google Scholar]
- Peng ZH, Wang D and Chen ZY et al. Adaptive dynamic surface control for formations of autonomous surface vehicles with uncertain dynamics. IEEE Trans Control Syst Technol 2013; 21: 513–20. [CrossRef] [Google Scholar]

Biao Ma received his B.S. degree in Aircraft Design and Engineering from the Nanjing University of Aeronautics and Astronautics (NUAA), Jiangsu, China, in 2020. He is currently pursuing his M.S. degree in Control Theory and Control Engineering from the NUAA. His current research interests include flight control and guidance.

Mou Chen received the B.S. degree in material science and engineering and Ph.D. degree in control theory and control engineering from the Nanjing University of Aeronautics and Astronautics (NUAA), Nanjing, China, in 1998 and 2004, respectively. He is currently a Full Professor with the College of Automation Engineering, NUAA. He was an Academic Visitor with the Department of Aeronautical and Automotive Engineering, Loughborough University, Loughborough, U.K., from November 2007 to February 2008. From June 2008 to September 2009, he was a Research Fellow with the Department of Electrical and Computer Engineering, National University of Singapore, Singapore. He was a Senior Academic Visitor with the School of Electrical and Electronic Engineering, University of Adelaide, Adelaide, SA, Australia, in 2014 for six months. His current research interests include nonlinear system control, intelligent control, and flight control.
All Figures
 |
Figure 1. The time-varying safety margin function changes over time |
| In the text | |
 |
Figure 2. Constrained desired trajectory generation process |
| In the text | |
 |
Figure 3. Upper and lower bounds of SFE. (a) Upper and lower bounds of attack angle, (b) Upper and lower bounds of slide angle and (c) Upper and lower bounds of roll angle |
| In the text | |
 |
Figure 4. The curve of attack angle during protection control |
| In the text | |
 |
Figure 5. The curve of slideslip angle during protection control |
| In the text | |
 |
Figure 6. The curve of roll angle during protection control |
| In the text | |
 |
Figure 7. The tracking errors of attitude angles during simulation. (a) The tracking error of attack angle, (b) the tracking error of slideslip angle and (c) The tracking error of roll angle |
| In the text | |
 |
Figure 8. Simulation details of attack angle during protection control |
| In the text | |
 |
Figure 9. Disturbances and their estimations. (a) dp and |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



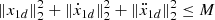
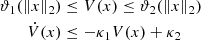





![$$ \begin{aligned} \left\{ \begin{array}{l} \hat{d}=z_1+k_1 x_2 \\ \dot{z}_1=-k_1\left[f_2\left(\bar{x}_2\right)+g_2\left(\bar{x}_2\right) u+\hat{d}\right]+\hat{\dot{d}} \\ \hat{\dot{d}}=z_2+k_2 x_2 \\ \dot{z}_2=-k_2\left[f_2\left(\bar{x}_2\right)+g_2\left(\bar{x}_2\right) u+\hat{d}\right]+\hat{\ddot{d}} \\ \qquad \vdots \\ \hat{d}^{(r-1)}=z_r+k_r x_2 \\ \dot{z}_r=-k_r\left[f_2\left(\bar{x}_2\right)+g_2\left(\bar{x}_2\right) u+\hat{d}\right] \end{array}\right. \end{aligned} $$](/articles/sands/full_html/2023/01/sands20230008/sands20230008-eq14.gif)



![$$ \begin{aligned} K=\left[\begin{array}{ccccc} k_1&-I_{3}&\cdots&0&0 \\ k_2&0&-I_{3}&\cdots&0 \\ \vdots&\vdots&\vdots&\vdots&\vdots \\ k_r&0&0&\cdots&0 \end{array}\right] \in \mathbb{R} ^{3r\times 3r} \end{aligned} $$](/articles/sands/full_html/2023/01/sands20230008/sands20230008-eq25.gif)
![$$ \begin{aligned} D^*=\left[0_{3}^{\mathrm{T} }, 0_{3}^{\mathrm{T} }, \ldots ,(d^{(r)})^{\mathrm{T} }\right]^{\mathrm{T} } \in \mathbb{R} ^{3r} \end{aligned} $$](/articles/sands/full_html/2023/01/sands20230008/sands20230008-eq26.gif)



![$$ \begin{aligned} \begin{aligned} \min J&= \dot{x}_1^\mathrm{{T}} S_1 \dot{x}_1+ [f_2\left(\bar{x}_2\right)+g_2\left(\bar{x}_2\right) u+\hat{d}(t)]^\mathrm{{T}} S_2 [f_2\left(\bar{x}_2\right)+g_2\left(\bar{x}_2\right) u+\hat{d}(t)] \\ \delta _{i, \min }&\le \delta _i \le \delta _{i, \max }, \ i \in \{a, c, r, y, z\} \end{aligned} \end{aligned} $$](/articles/sands/full_html/2023/01/sands20230008/sands20230008-eq33.gif)














![$$ \begin{aligned} e_{\rm \Omega }&=[e_{\alpha }, e_{\beta }, e_{\mu }]^{\mathrm{T} }=x_1-x_{1s} \\ e_\omega&=x_2-x_2^* \end{aligned} $$](/articles/sands/full_html/2023/01/sands20230008/sands20230008-eq53.gif)

![$$ \begin{aligned} \varepsilon _{i}=S_i^{-1}\left(\frac{e_{i}(t)}{\rho _i(t)}\right)= {\left\{ \begin{array}{ll}\frac{1}{2} \ln \frac{z_i+\delta _i}{1-z_i},&e_i(0) \ge 0 \\ [3pt] \frac{1}{2} \ln \frac{z_i+1}{\delta _i-z_i},&e_i(0)<0\end{array}\right.} \end{aligned} $$](/articles/sands/full_html/2023/01/sands20230008/sands20230008-eq55.gif)



![$$ \begin{aligned} \begin{aligned} \dot{\varepsilon }_{\mathrm{\Omega }}&=R(t) \dot{e}_{\mathrm{\Omega }}-N(t) \\&=R(t)\left[f_1\left(x_1\right)+g_1\left(x_1\right) e_\omega +g_1\left(x_1\right) x_2^*-\dot{x}_{1s}\right]-N(t) \end{aligned} \end{aligned} $$](/articles/sands/full_html/2023/01/sands20230008/sands20230008-eq61.gif)
![$$ \begin{aligned} x_2^*=g_1^{-1}\left(x_1\right)\left[-f_1\left(x_1\right)+\dot{x}_{1s}+R^{-1}(t) N(t)-R^{-1}(t) K_{\mathrm{\Omega }} \varepsilon _{\mathrm{\Omega }}\right] \end{aligned} $$](/articles/sands/full_html/2023/01/sands20230008/sands20230008-eq62.gif)


![$$ \begin{aligned} \begin{aligned} \dot{V}_{\mathrm{\Omega }} =\varepsilon _{\mathrm{\Omega }}^{\mathrm{T} } \dot{\varepsilon }_{\mathrm{\Omega }}&=\varepsilon _{\mathrm{\Omega }}^{\mathrm{T} }\left[-K_{\rm \Omega } \varepsilon _{\rm \Omega }+R(t) g_1\left(x_1\right) e_\omega \right] =-\varepsilon _{\rm \Omega }^{\mathrm{T} } K_{\rm \Omega } \varepsilon _{\rm \Omega }+\varepsilon _{\rm \Omega }^{\mathrm{T} } R(t) g_1\left(x_1\right) e_\omega \end{aligned} \end{aligned} $$](/articles/sands/full_html/2023/01/sands20230008/sands20230008-eq68.gif)

![$$ \begin{aligned} u=g_2^{-1}\left(\bar{x}_2\right)\left[-f_2\left(\bar{x}_2\right)-\hat{d}+\dot{x}_2^*-K_\omega e_\omega -g_1^{\mathrm{T} }\left(x_1\right) R^{\mathrm{T} }(t) \varepsilon _{\rm \Omega }\right] \end{aligned} $$](/articles/sands/full_html/2023/01/sands20230008/sands20230008-eq70.gif)


![$$ \begin{aligned} \begin{aligned} \dot{V}_\omega&=e_\omega ^{\mathrm{T} } \dot{e}_\omega +\dot{V}_d(\tilde{D}) =e_\omega ^{\mathrm{T} }\left[-K_\omega e_\omega -\tilde{d}-g_1^{\mathrm{T} }\left(x_1\right) R^{\mathrm{T} }(t) \varepsilon _{\rm \Omega }\right]+\dot{V}_d(\tilde{D}) \\&=-e_\omega ^{\mathrm{T} } K_\omega e_\omega -e_\omega ^{\mathrm{T} } \tilde{d}-e_\omega ^{\mathrm{T} } g_1^{\mathrm{T} }\left(x_1\right) R^{\mathrm{T} }(t) \varepsilon _{\rm \Omega }+\dot{V}_d(\tilde{D}) \\&\le -e_\omega ^{\mathrm{T} }\left(K_\omega -0.5 I\right) e_\omega -e_\omega ^{\mathrm{T} } g_1^{\mathrm{T} }\left(x_1\right) R^{\mathrm{T} }(t) \varepsilon _{\rm \Omega }-\tilde{D}^{\mathrm{T} }\left(K-I\right) \tilde{D}+0.5 \eta _{r}^2 \end{aligned} \end{aligned} $$](/articles/sands/full_html/2023/01/sands20230008/sands20230008-eq76.gif)