| Issue |
Security and Safety
Volume 2, 2023
Security and Safety in Unmanned Systems
|
|
|---|---|---|
| Article Number | 2023016 | |
| Number of page(s) | 15 | |
| Section | Information Network | |
| DOI | https://doi.org/10.1051/sands/2023016 | |
| Published online | 23 August 2023 | |
Research Article
Communication security of autonomous ground vehicles based on networked control systems: The optimized LMI approach
1
Cyberspace Institute of Advanced Technology, Guangzhou University, Guangzhou, 510006, China
2
School of Electronic Information and Electrical Engineering, Chengdu University, Sichuan, 610106, China
3
School of Information and Software Engineering, University of Electronic Science and Technology of China, Chengdu, 611731, China
4
School of Mathematics Sciences, University of Electronic Science and Technology of China, Chengdu, 611731, China
5
Faculty of Engineering and Information Technology, Australian AI Institute, University of Technology Sydney, Ultimo, NSW 2007, Australia
* Corresponding authors (email: caixiao327327@163.com (Xiao Cai); skbs111@163.com (Kaibo Shi))
Received:
2
January
2023
Revised:
16
March
2023
Accepted:
19
June
2023
The paper presents a study of networked control systems (NCSs) that are subjected to periodic denial-of-service (DoS) attacks of varying intensity. The use of appropriate Lyapunov–Krasovskii functionals (LKFs) help to reduce the constraints of the basic conditions and lower the conservatism of the criteria. An optimization problem with constraints is formulated to select the trigger threshold, which is solved using the gradient descent algorithm (GDA) to improve resource utilization. An intelligent secure event-triggered controller (ISETC) is designed to ensure the safe operation of the system under DoS attacks. The approach is validated through experiments with an autonomous ground vehicle (AGV) system based on the Simulink platform. The proposed method offers the potential for developing effective defense mechanisms against DoS attacks in NCSs.
Key words: Networked control system / autonomous ground vehicle / cyber security / optimized LMI approach / event-trigger control
Citation: Cai X, Shi K and She K et al. Communication security of autonomous ground vehicles based on networked control systems: The optimized LMI approach. Security and Safety 2023; 2: 2023016. https://doi.org/10.1051/sands/2023016
© The Author(s) 2023. Published by EDP Sciences and China Science Publishing & Media Ltd.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The 21st century has seen rapid development in network communication technology, which has revolutionized numerous fields, including industrial control. The integration of control theory, control technology, computer technology, and network communication technology has facilitated the growth of networked control systems (NCSs) [1, 2]. NCSs have been extensively utilized in diverse applications, as illustrated in Figure 1, and have emerged as the preferred technology due to the incorporation of communication and computer technology into the Internet-based TCP/IP protocol [3, 4].
 |
Figure 1. Networked control systems and application |
The proposal of NCSs has allowed for the organic combination of regional control nodes and devices, breaking the information island phenomenon of traditional control systems. This approach expands the way information is transmitted and enables the diversification of management, monitoring, and control strategies across different regions while simplifying the system’s design and improving its reliability and flexibility [5, 6]. NCSs offer the favored development direction for future industrial control systems as they can add or delete control inputs and sensors as nodes are added or removed, offering the ability to modify and adapt the system to meet evolving requirements. Recent research on NCSs has focused on information transmission security, covert false data injection attacks, and network protocol and bandwidth selection to ensure that important closed-loop properties are maintained when inserting computer networks into feedback loops [7–9]. In [7], the author studied the information transmission security problem of NCSs. In [8], the design and detection of covert false data injection attacks against NCSs were studied from different perspectives of attackers and defenders. In [9], the authors investigated the choice of network protocols and bandwidth for NCSs to ensure that important closed-loop properties are preserved when inserting computer networks into feedback loops.
The security of NCSs can be classified into three main areas, namely information security, functional safety, and physical security [10]. Initially, functional and physical safety received more attention to prevent equipment or control system failures [11, 12]. Even in the event of equipment failure, the system should still be able to enter a safe, normal operating state. However, with the widespread adoption of Internet communication technology in industrial control systems, the significance of information security has become more prominent, and the industry has shifted its focus toward it [13]. Previous studies have proposed various approaches to mitigating the impact of denial-of-service (DoS) attacks on NCSs. For example, in [4], the authors proposed an improved approach to estimate performance errors caused by DoS attacks in T-S fuzzy NCSs using suitable integral elastic event-triggered mechanisms and improved Lyapunov–Krasovskii functionals (LKFs). In [14], a resilient event-triggered strategy was proposed for nonlinear NCSs with interval type-2 fuzzy models subject to nonperiodic DoS attacks, which aimed to reduce performance loss. The authors used a new mismatched membership function to simplify the network control structure under DoS attacks. In [15], an event-triggered control method was presented to analyze the impact of DoS attacks on NCSs in two cases: with and without DoS attacks. The authors in [16] proposed the security control problem of NCSs under DoS attacks as a critical research topic. Moreover, Cheng et al. [17] found that DoS attacks are periodic and studied the relationship between DoS periodic attacks and decay rates.
This paper proposes a periodic DoS attack with an attacking intensity and studies its impact on NCSs, building upon previous research. The study of DoS attacks is crucial for the security of NCSs due to the increasing prominence of information security issues resulting from the application and development of Internet communication technology in industrial control systems. As a result, there is a growing emphasis on information security in the industry, and researchers are actively developing strategies to mitigate the impact of DoS attacks on NCSs. Intelligent transportation systems heavily rely on autonomous ground vehicles (AGVs), which integrate various high-tech technologies that have been the subject of extensive research [18, 19]. AGVs consist of multiple systems and technologies, including expert system planning functions, computer vision, autonomous navigation, and advanced parallel processing. AGVs can make independent judgments and plans, accept tasks in natural language, devise task execution methods, and continuously revise their plans. This design concept enables AGVs to complete tasks autonomously, even in complex terrain [20]. AGV control systems, as a new interdisciplinary field, can benefit from the use of NCSs, a novel type of control technology that relies on the Internet after the industrialized control system [21]. Therefore, combining NCSs with AGV control systems is an area of significant importance for research.
Based on the previous discussion, this paper focuses on the basic theory of NCSs and AGVs and conducts research on information security and intelligent secure event-triggered controller (ISETC) design issues for AGVs. The main contributions to this paper are summarized below:
-
(1)
The paper proposes a model for NCSs under periodic DoS attacks with varying attack intensity. Suitable LKFs are constructed, and an optimized Linear Matrix Inequality (LMI) is used to analyze the stability of NCSs.
-
(2)
The paper transforms the selection of the trigger threshold into an optimization problem with constraints and employs gradient descent algorithm (GDA) to optimize the threshold and ensure maximum utilization of sampling resources.
-
(3)
An ISETC is designed for AGV’s network communication. The ISETC is used to analyze the security and stability of the system and ensure that data transmission is not affected by malicious attacks.
Notation: Sym{Q} denotes Q + QT. ℝm × n denotes the set of m × n real matrices. In is the n × n identity matrix. M > 0(≥0) indicates M is a positive definite matrix. diag{A1, A2, …, An} indicates a diagonal matrix and the diagonal elements are Ai, i = 1, 2, …, n. P−1 indicates the inverse P. PT is the transpose of matrix P. ℝn is the n-dimensional Euclidean space.
2. Preliminaries
A. Event-trigger control and design of DoS attacks
In this paper, we focus on the study of NCSs that are subject to external disturbances as follows:
where x(t)∈ℝn means the current state vector; u(t)∈ℝm is the signal to control the input; the external disturbance is ω(t)∈𝔏2[0, ∞); 𝒜, ℬ, 𝒞 are constant matrices.
In addition to external disturbances, this paper also examines the security of NCSs during network communication transmission. Specifically, we focus on the design of an ISETC to address DoS attacks that occur periodically and with varying levels of intensity. To model these attacks, we assume that the system is targeted by hackers at regular intervals, with tkh representing the instantaneous sampling time point. The DoS attack design is based on prior research [22]:
where 𝒢 is attack intensity; δ(t − tkh) means Dirac function. The  and limk → ∞tkh = ∞ is periodic attack signals.
and limk → ∞tkh = ∞ is periodic attack signals.  , where
, where  and
and  . This paper assumes that x(t) is right continuous, then we get
. This paper assumes that x(t) is right continuous, then we get  and has a left limit and the DoS attack interval is shown in Definition 1.
and has a left limit and the DoS attack interval is shown in Definition 1.
The ZOH function generates a sequence of control signals where the sampling instant tkh satisfies 0 = t0 < t1h < t2h < ⋯ < tkh < ⋯, tk + 1h (k ∈ [0, ∞)). Assuming that the sampling period satisfies 0 ≤ hm < tk + 1h − tkh ≜ hk ≤ hM, and ∀k ≥ 0. Then, we assume that x(tkh) is the value of the current state of the system thread;  is the system thread state of the last successful transmission of the system. We have
is the system thread state of the last successful transmission of the system. We have
where e(tkh) indicates the error between the current thread state of the system and the system thread state of the system’s last successful transmission.
Attacks launched by hackers may cause errors in the trigger control of the system, as shown in Figure 2. To capture the impact of such attacks, we assume that  represents the system thread state at the last successful transmission following a DoS attack. The error is defined as follows:
represents the system thread state at the last successful transmission following a DoS attack. The error is defined as follows:
 |
Figure 2. Event-trigger under DoS attacks |
where σ ∈ ℕ, e(tkh) represents the error between the current state of the system and the last successful transmission state when the hacker attacks.
Based on the above analysis, a new ETC is designed as follows [14]:
where
and Φ > 0 is a weighting matrix; ρ indicates a threshold parameter; 𝒢 means attack strength.
Defined the delay at every two successful sampling moments τ ≜ t − tkh. Then, the control signal is designed as follows:
Based on the analysis of (1)–(5), we can get the following NSCs:
where 𝒦 is a controller gain matrix.
We considered the vulnerabilities of the ISETC in the presence of external attacks and proposed a novel approach to mitigate the effects of a periodic DoS attack ϕtkh with varying strengths 𝒢. Unlike the existing methods proposed in [15, 23], our approach takes into account the attack’s periodicity and strength, which has important implications for developing effective defense mechanisms. By studying the behavior of the system under such attacks, we were able to design a robust and secure ISETC that provides reliable communication in the presence of adversarial interference.
B. Parameter optimization based on gradient descent algorithm
Selecting an appropriate threshold parameter ρ is a crucial aspect of trigger threshold design. The optimization of trigger threshold selection is a complex problem that can be formulated as an optimization problem with constraints. Based on optimization methods in several studies [24, 25], we also propose an optimal scheme for designing and optimizing trigger threshold selection. The main objective of the scheme is to maximize the utilization of the available sampling resources, subject to the satisfaction of system performance and stability constraints. The following constraint problem is posed:
where ρ is the threshold parameter that needs to be determined. F(ρ):ℝn → ℝ is the objective function. g(ρ):ℝn → ℝm denotes a vector function for solving inequality constraint problems at ρ. ρl and ρu represent the upper and lower bounds of ρ, respectively.
Then, the gradient descent method is used to optimize the target problem by updating the threshold parameter iteratively. At each iteration, the step length is set as ρk + 1 = ρk + mk, where mk is the step size and lkρk is the descent direction. The optimal threshold parameter is obtained when the objective function reaches its minimum value.
The parameter ρk is necessary for Pareto optimization, as there is no first-order descending direction for all individual goals. For all individual goals, there is no first-order descending direction as follows:
where  is said to the pyramid, TH(ρk) is H in ρk of the jacobian matrix. When n = 1, lk = −∇h1(ρk) for the fastest decline in the direction, which is equivalent to minimizing threshold
is said to the pyramid, TH(ρk) is H in ρk of the jacobian matrix. When n = 1, lk = −∇h1(ρk) for the fastest decline in the direction, which is equivalent to minimizing threshold  in l.
in l.
It is proved that the dual of (10) is a sub-problem
where  is a simplex set. According to the theory in [25], we get the following
is a simplex set. According to the theory in [25], we get the following
In accordance with the approach described in references [24, 25], selecting an appropriate threshold parameter ρ is crucial for Pareto maximization. To address this problem, we transform the process into an optimization problem, which enables us to iteratively determine the optimal threshold parameter that satisfies the system requirements. By employing the gradient descent algorithm, we accelerate the search for the threshold parameter, resulting in optimized parameters that reduce the trigger rate and save sampling resources. This method has been proven effective in expediting the search process and enhancing the system’s performance.
The Pareto first-order stationary point, denoted as ρk ∈ ℙ, is obtained by solving the optimization problem in equation (8) using the proximal gradient algorithm. This iterative algorithm updates the estimate of the Pareto front using the gradient of the objective function and the proximal operator of the regularization term. The proximal operator enforces the constraint that the estimate of the Pareto front belongs to the feasible set ℙ. The algorithm continues to update the estimate of the Pareto front until convergence is achieved, which is determined by a stopping criterion based on the norm of the difference between successive estimates of the Pareto front. The algorithm also includes a step size parameter mk, which controls the step size of the gradient descent update. This parameter is chosen using a backtracking line search that ensures the update decreases the objective function. The specific steps of the algorithm are as follows:
Input: ρk ∈ [ρl, ρu] ⊆ S and a step size sequence mk
Output: ρk+1
1 begin
2 for k = 0,1, … do
3 Compute the gradients
4 ∃λ ∈ ∆n → gk(ρ) = Σni=1 λi∇hi(ρk) = 0
5 Solve the objective function
6 λk ∈ arg maxλ∈ℝn ∥ Σni=1 λi∇hi(ρk)∥2
7 λ ∈ {λ : Σni=1 λi, λi ≥ 0, ∀i = 1, …, m}
8 Iterative the next updates ρk+1
9 ρk+1 = ℙS (ρk – mkgk(ρ))
10 end
11 end
[26] The average DoS attacks interval of the attack time sequence ϑ = {t1, ⋯, tk, ⋯} is equal to Ta if there exist S0 ≥ 0 and Ta, we can get the DoS attacks interval as follow:
where ∀T ≥ t ≥ 0 and Nϑ(T, t) is the total number of times the attack sequence ϑ has been hacked over the time period (t, T).
[27] Given a x satisfies x : [a, b]→ℝn. And there are the arbitrary matrices N1, N2 and N3 and the matrices M > 0. We can get the following inequality holds:
where
3. Main results
In this section, we consider the scenario where the control gain matrix 𝒦 is known and establish the asymptotic stability condition of the system under the designed safe trigger mechanism, which is presented in Theorem 1. We then proceed to design and solve the controller gain matrix in Theorem 2. To simplify the notation, we define the following symbols:
Let hM, hm, and ρ be positive scalars. The NCSs given by (7) are asymptotically stable if there exist symmetric matrices 𝒫, ℋ, any matrix of suitable dimension ℳ, 𝒬, and 𝒴n (n = 1, 2, 3) that satisfy the following LMIs:
where
Given the LKFs candidate as
where
We take the derivative of Vi(t), and we get
Using the integral inequality in Lemma 1, the integral term in (17) can be scaled as follows:
Based on the above results,  can be rewritten as follows:
can be rewritten as follows:
The constraints of the unsafe ISETC (5) are considered, and the following inequality is obtained:
Based on the system (7), the following equation is got
According to (14)–(21), the following equation is had as follow
Based on the linear convex combinations method [28], for all ξT(t)Ξξ(t)< 0 are established. We can get
Finally, we can conclude that the NCSs (7) are asymptotically stable if the conditions (11) of Theorem 1 are satisfied and if the inequality  holds. This inequality ensures that the LKF V(t) is decreasing along the system trajectory, and therefore, the system state will converge to the equilibrium point. Thus, the designed safe trigger mechanism ensures the asymptotic stability of the NCSs in the presence of DoS attacks.
holds. This inequality ensures that the LKF V(t) is decreasing along the system trajectory, and therefore, the system state will converge to the equilibrium point. Thus, the designed safe trigger mechanism ensures the asymptotic stability of the NCSs in the presence of DoS attacks.
Unlike the method in reference [29], the sampling time information is fully considered in the looped function constructed by V2(t). It contains both the date information on x(tkh) and x(tk + 1h), satisfying 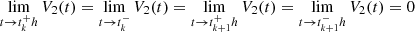 . This method introduces more sampling time information based on reducing the initial constraints. Furthermore, increasing the information storage of LKFs reduces the conservatism of the criteria.
. This method introduces more sampling time information based on reducing the initial constraints. Furthermore, increasing the information storage of LKFs reduces the conservatism of the criteria.
Analyzing the computational complexity of control algorithms is essential. In this paper, a loop function is constructed to reduce the initial constraints and therefore decrease the computational complexity of the control algorithm. The resulting algorithm achieves effective control of AGVs with relatively low computational complexity, specifically 6n2 + n. Moreover, we were able to verify the results within an acceptable time using an Intel(R) Core(TM) i7-8565U CPU @ 1.80 GHz 1.99 GHz computer.
The control algorithm considers stability analysis and employs an optimization approach to determine the maximum allowable delay and the controller gain matrix. This guarantees the system’s stability under DoS attacks while minimizing their impact on the system’s performance. Control Algorithm 2 is based on the presented stability analysis, and it aims to calculate the maximum allowable delay τmax and the controller gain matrix K to ensure the system’s stability under DoS attacks. The algorithm is outlined as follows:
Input: The known positive definite vector ρ, hm, hM, µ1, 𝒢 and µ2
Output: The maximum acceptable time delay τmax and controller gain matrix 𝒦
1 Initialize the global counter δi;
2 Reset maximum acceptable time delay τmax;
3 for δi = 0 : 0.0001 : 1 do
4 𝒫 ≥ 0, ℋ > 0, Ξ ≤ 0,
5 if There is not a feasible solution then
6 Replace τmax with τmax + δi;
7 Replace δi with δi+1;
8 Return Line 4
9 else break
10 end
11 end
Let ρ, μ1, μ2, hm, and hM be positive scalars. Consider the NCSs (7) under the designed safe trigger mechanism. The system is asymptotically stable if there exist symmetric matrices 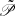 ,
, 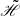 , and any matrices
, and any matrices 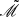 ,
, 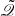 , and 𝒲 that satisfy the following LMIs:
, and 𝒲 that satisfy the following LMIs:
where
The gain matrix 𝒦 = 𝒲𝒳−1 and  are defined. Pre-multiplying and post-multiplying (13) by
are defined. Pre-multiplying and post-multiplying (13) by
Then, the LMIs (23) can be obtained. The detailed proof process is similar to Theorem 1.
4. Illustrative example
We conducted simulation experiments on the Simulink joint platform to verify the effectiveness of the proposed control algorithm in this paper, using the data provided in reference [19]. The experimental setup is illustrated in Figure 3, and some data related to the vehicle are shown in Table 1:
 |
Figure 3. Schematic diagram of path following model |
Parameter values of the autonomous ground vehicles
The dynamic physics equations for AGV (see Figure 3) can be written as follows:
Set the state vector is x(t)=[e, ϕ, ϖ, r]T, the control input signal is u(t)=σf and the external disturbance ω(t)=[s1, −ρ(δc)vx, s2, s3]T. Finally, the physical state space model of AGV is expressed as follows:
where
The experimental setup was conducted on the Simulink joint platform to verify the effectiveness of the proposed control algorithm in this paper using the data provided in reference [19]. The physical meanings of the parameters were defined in [19]. Specifically, m denotes the weight of the vehicle, Is is the yaw inertia of the vehicle, ln represents the distance from the rear wheel to the center of gravity, lm indicates the distance from the front wheel to the center of gravity, and Cn and Cm denote the cornering stiffness of the front and rear tires, respectively. We set the intensity to 𝒢 = 10, with an attack period of 0.1, and assume that hm = 0 and ρ = 0.5. To evaluate the impact of varying hM on the system, we used the Yalmip toolbox to solve for the maximum acceptable time delay τmax.
The maximum acceptable time delay τmax under different preset sampling periods h
As shown in Table 2, the proposed control algorithm in this paper has a maximum acceptable delay limit of 1.3821 when hM = 0.4. In contrast, reference [19] limits the maximum acceptable latency to τmax = 0.04. This comparison clearly demonstrates the superior performance of the proposed algorithm in dealing with system delays and DoS attacks. The impact of DoS attacks on system performance is further studied, and we conduct simulations with different attack strengths and maximum delay constraints. Specifically, we set hM = 0.2 and examined the maximum acceptable delay of the DoS attack system under different attack strengths. The results are presented in Table 3, where we observe that the maximum acceptable time delay of the system changes with varying attack strengths. Notably, when the attack strength is set to 𝒢 = 10, the maximum transmission time delay of the system is τmax = 0.5963. These results indicate the importance of implementing robust control strategies in NCSs that can handle and mitigate the effects of attacks, especially high-intensity DoS attacks. The proposed control algorithm in this paper has a computational complexity of 6n2 + n, which means that the system’s asymptotic stability can be ensured even with a low number of decision variables. Moreover, the low computational complexity of the control algorithm reduces processing time and energy consumption, making it more feasible for real-time control applications. In summary, the proposed control algorithm not only guarantees the system’s stability and security but also provides practical benefits by minimizing the computational burden and optimizing resource allocation.
The maximum acceptable time delay τmax under different DoS attack strength
Then, the control gain matrix K = 104[2.0171 −1.9720 −0.9823 −0.6937] was obtained using the method in Theorem 2 when the parameters μ1 and μ2 were set to 1. This control gain matrix was then used in a Simulink joint platform simulation experiment to verify the feasibility of the proposed control design method. The results presented in Figures 4 and 5 demonstrate that the proposed control design method is effective in mitigating the impact of DoS attacks on the system, as the system can still converge smoothly under the designed controller and control algorithm, even when subjected to DoS attacks with high intensity and a short attack period. Furthermore, the study found that the proposed control design method is more effective than the method presented in [19], as it enables the system to tolerate a higher maximum delay limit under DoS attacks, as shown in Table 2. These results provide valuable insights into the development of robust control algorithms for NCSs that are vulnerable to DoS attacks, highlighting the importance of implementing such algorithms to ensure system stability and security. Additionally, the proposed control algorithm has relatively low computational complexity, making it a practical solution for real-time control applications.
 |
Figure 4. System parameter state trajectory response with DoS attacks |
 |
Figure 5. System parameter state trajectory response without DoS attacks |
Furthermore, selecting appropriate trigger thresholds is crucial for mitigating DoS attacks in practice. In this paper, we propose a novel approach based on GDA for optimizing trigger thresholds. By formulating the threshold selection as a constrained optimization problem, we can find optimal thresholds that minimize the trigger rate of legitimate traffic while maintaining high mitigation of DoS attacks. First, we iterate through the ρk values using the Python toolbox and then bring the results into the Yalmip toolbox for solving. This learning algorithm significantly improves resource efficiency by iteratively searching for a suitable value of ρk. The intelligent trigger threshold search mechanism employs machine learning to find the optimal threshold, denoted by ρ, by iteratively traversing the range [0, 1] as shown in the sequence ρ1 → ⋯ → ρ2 → ⋯ → ρk − 1 → ⋯ → ρk → ⋯. In this way, the algorithm iteratively learns and searches for the ρk with the lowest trigger rate. Additionally, we present the number of system triggers under GDA and traditional algorithms are in Figures 6 and 7, respectively. Our results show that GDA-optimized thresholds can significantly reduce the number of false triggers compared to the conventional method, resulting in a lower trigger rate of 86.62% for GDA versus 88.5% for the traditional algorithm. These findings demonstrate the effectiveness of our proposed approach in reducing the impact of DoS attacks on network performance.
 |
Figure 6. Release instants and time intervals under GDA |
 |
Figure 7. Release instants and time intervals under regular algorithm |
Finally, the optimized trigger thresholds can also provide additional benefits in terms of resource allocation and system resilience. By reducing the number of false triggers, our approach can free up more resources for other tasks or mitigate the impact of DoS attacks on system performance. In a word, our approach can enhance the security and reliability of network systems in the face of increasingly sophisticated DoS attacks.
5. Conclusion
This paper addressed the issue of NCSs under DoS attacks with periodicity and attack intensity. The research on the power of the DoS attacks was significant for establishing suitable defense mechanisms. The paper presented a method to construct appropriate LKFs, reducing the constraints of basic conditions and mitigating criterion conservatism. Additionally, the paper transformed the selection problem of the trigger threshold into an optimization problem with constraints and used the GDA to optimize the threshold, saving sampling resources. An ISETC was designed to ensure the normal operation of AGVs under DoS attacks. Finally, the proposed method’s effectiveness was verified by simulating the AGVs system based on the Simulink platform. In the future, further research could focus on developing more sophisticated defense mechanisms to protect NCSs from different types of cyber-attacks and enhancing the performance and robustness of AGVs systems under various adverse conditions.
Conflict of Interest
No conflict of interest exists in the submission of this manuscript, and the manuscript is approved by all authors for publication. I would like to declare on behalf of my co-authors that the work described was original research that has not been published previously and is not under consideration for publication elsewhere, in whole or in part. All the authors listed have approved the manuscript that is enclosed.
Data Availability
We make data available on request through sending an email to the authors.
Authors’ Contributions
Xiao Cai and Yuanlun Xie contributed to the conception of the study; Xiao Cai performed the experiment and the data analyses and wrote the manuscript; Kaibo Shi contributed significantly to the analysis and manuscript preparation; Kun She contributed significantly to the methodology and presentation of the manuscript; Shouming Zhong helped perform the analysis with constructive discussions.
Acknowledgments
We thank all anonymous reviewers for their helpful comments and suggestions.
Funding
This work was supported by the National Key Research and Development Plan (Grant No. 2020YFB2009503), the National Natural Science Foundation of China under Grant (Nos. 61703060, 61802036, 61701048, 61873305, U20B2046, 62272119, 62072130), the Sichuan Science and Technology Program under Grant No. 2021YJ0106, the Guangdong Basic and Applied Basic Research Foundation (Nos. 2020A1515010450, 2021A1515012307), Guangdong Province Universities and Colleges Pearl River Scholar Funded Scheme (2019), and Guangdong Higher Education Innovation Group (No. 2020KCXTD007), Guangzhou Higher Education Innovation Group (No. 202032854), Consulting project of the Chinese Academy of Engineering (2022-JB-04-05).
References
- Bemporad A, Heemels M and Johansson M. Networked Control Systems. Vol. 406. London: Springer, 2010. [CrossRef] [Google Scholar]
- Gupta RA and Chow MY. Networked control system: overview and research trends. IEEE Trans Ind Electron 2009; 57: 2527–35. [Google Scholar]
- Walsh GC and Ye H. Scheduling of networked control systems. IEEE Control Syst Mag 2001; 21: 57–65. [CrossRef] [Google Scholar]
- Cai X, Shi K and She K et al. Performance error estimation and elastic integral event triggering mechanism design for T-S fuzzy networked control system under DoS attacks. IEEE Trans Fuzzy Syst 2022; 31: 1327–39. [Google Scholar]
- Wang F-Y and Liu D. Networked Control Systems. London: Springer, 2008. [CrossRef] [Google Scholar]
- Zhang W, Branicky MS and Phillips SM. Stability of networked control systems. IEEE Control Syst Mag 2001; 21: 84–99. [CrossRef] [Google Scholar]
- Cai X, Shi K and She K et al. Quantized sampled-data control tactic for T-S fuzzy NCS under stochastic cyber-attacks and its application to truck-trailer system. IEEE Trans Veh Technol 2022; 71: 7023–32. [CrossRef] [Google Scholar]
- Pang Z-H, Fan L-Z and Sun J et al. Detection of stealthy false data injection attacks against networked control systems via active data modification. Inf Sci 2021; 546: 192–205. [CrossRef] [Google Scholar]
- Walsh GC, Beldiman O and Bushnell LG. Asymptotic behavior of nonlinear networked control systems. IEEE Trans Autom Control 2001; 46: 1093–97. [CrossRef] [Google Scholar]
- Sandberg H, Amin S and Johansson KH. Cyberphysical security in networked control systems: an introduction to the issue. IEEE Control Syst Mag 2015; 35: 20–3. [Google Scholar]
- Zeng W and Chow M-Y. Optimal tradeoff between performance and security in networked control systems based on coevolutionary algorithms. IEEE Trans Ind Electron 2011; 59: 3016–25. [Google Scholar]
- Kogiso K and Fujita T. Cyber-security enhancement of networked control systems using homomorphic encryption. In: 2015 54th IEEE Conference on Decision and Control (CDC). IEEE, 2015, 6836–43. [CrossRef] [Google Scholar]
- Zhang L, Gao H and Kaynak O. Network-induced constraints in networked control systems-a survey. IEEE Trans Ind Inf 2012; 9: 403–16. [Google Scholar]
- Pan Y, Wu Y and Lam H-K. Security-based fuzzy control for nonlinear networked control systems with DoS attacks via a resilient event-triggered scheme. IEEE Trans Fuzzy Syst 2022; 30: 4359–68. [CrossRef] [Google Scholar]
- Peng C and Sun H. Switching-like event-triggered control for networked control systems under malicious denial of service attacks. IEEE Trans Autom Control 2020; 65: 3943–49. [CrossRef] [Google Scholar]
- Amin S, Cardenas AA and Sastry SS. Safe and secure networked control systems under denial-of-service attacks. In: Hybrid Systems: Computation and Control: 12th International Conference, HSCC 2009, San Francisco, CA, USA, April 13–15, 2009. Proceedings 12. Springer Berlin Heidelberg, 2009, 31–45. [Google Scholar]
- Hu S, Yue D and Xie X et al. Resilient event-triggered controller synthesis of networked control systems under periodic DoS jamming attacks. IEEE Trans Cybern 2018; 49: 4271–81. [Google Scholar]
- Ozguner U, Acarman T and Redmill KA. Autonomous Ground Vehicles. London: Artech House, 2011. [Google Scholar]
- Wang R, Jing H and Hu C et al. Robust H∞ path following control for autonomous ground vehicles with delay and data dropout. IEEE Trans Intell Transp Syst 2016; 17: 2042–50. [CrossRef] [Google Scholar]
- Wu Y, Wang L and Zhang J. Path following control of autonomous ground vehicle based on nonsingular terminal sliding mode and active disturbance rejection control. IEEE Trans Veh Technol 2019; 68: 6379–6390. [CrossRef] [Google Scholar]
- Eskandarian A, Wu C and Sun C. Research advances and challenges of autonomous and connected ground vehicles. IEEE Trans Intell Transp Syst 2019; 22: 683–711. [Google Scholar]
- He W, Qian F and Han Q-L et al. Almost sure stability of nonlinear systems under random and impulsive sequential attacks. IEEE Trans Autom Control 2020; 65: 3879–86. [CrossRef] [Google Scholar]
- Peng C and Sun H. Switching-like event-triggered control for networked control systems under malicious denial of service attacks. IEEE Trans Autom Control 2020; 65: 3943–9. [CrossRef] [Google Scholar]
- Plevris V and Papadrakakis M. A hybrid particle swarm-gradient algorithm for global structural optimization. Comput. Aided Civil Infrastruct Eng 2011; 26: 48–68. [Google Scholar]
- Liu S and Vicente LN. The stochastic multi-gradient algorithm for multi-objective optimization and its application to supervised machine learning. Ann Oper Res 2021; 1–30, doi: 10.1007/s10479-021-04033-z. [Google Scholar]
- Lu J, Jiang B and Zheng WX. Potential impacts of delay on stability of impulsive control systems. IEEE Trans Autom Control 2021; 67: 5179–90. [Google Scholar]
- Cai X, Shi K and She K et al. Reliable sampling mechanism for Takagi-Sugeno fuzzy NCSs under deception cyberattacks for the application of the inverted pendulum system. IEEE Trans Reliab 2022, doi: 10.1109/TR.2022.3215075. [Google Scholar]
- Cai X, Shi K and She K et al. Event-triggered control strategy for 2-DoF helicopter system under DoS attacks. IEEE Trans Transp Electr 2023; 9: 3240–54. [CrossRef] [Google Scholar]
- Hu S, Yue D and Xie X et al. Resilient event-triggered controller synthesis of networked control systems under periodic DoS jamming attacks. IEEE Trans Cybern 2018; 49: 4271–81. [Google Scholar]

Xiao Cai is currently a Ph.D. candidate at the University of Electronic Science and Technology of China, Chengdu, China. From September 2021 to September 2022, he was a visiting scholar with the Department of Electrical Engineering, Pohang University of Science and Technology, Pohang, South Korea. From November 2022 to November 2023, he is currently a visiting researcher with the School of Electrical & Electronic Engineering, Nanyang Technological University, Singapore. His current research interests include stability theorem, robustness stability, robust control, event trigger control, networked control systems, cyber-physical systems, optimized control and cyber security.

Kaibo Shi received a Ph.D. degree from the School of Automation Engineering, University of Electronic Science and Technology of China, Chengdu, China, in 2016. From September 2014 to September 2015, he was a Visiting Scholar with the Department of Applied Mathematics, University of Waterloo, Waterloo, ON, Canada. He was a Research Assistant with the Department of Computer and Information Science, Faculty of Science and Technology, University of Macau, Taipa, from May 2016 to June 2016 and January 2017 to October 2017. He is currently an Associate Professor at the School of Information Sciences and Engineering, at Chengdu University. His current research interests include the stability theorem, robustness stability, robust control, sampled-data control, synchronization, Lurie chatic system, stochastic systems, and neural networks.

Kun She received a B.Sc. degree in applied mathematics from the University of Electronic Science and Technology of China, Chengdu, Sichuan, China, in 1989, an M.Sc. degree in electronic and communication systems from the Southwest Institute of Communications, in 1992, and a Ph.D. degree in computer science from the University of Electronic Science and Technology of China. He is currently a Professor at the University of Electronic Science and Technology of China. Since 2006, he has been a Visiting Professor with the Illinois University of Technology. His research interests include intelligent computing, cloud computing, big data, network security, and network engineering.

Shouming Zhong was born in 1955. He received a graduate degree in applied mathematics in differential equations from the University of Electronic Science and Technology of China, Chengdu, China, in 1982. He has been a Professor at the School of Mathematical Sciences, University of Electronic Science and Technology of China since 1997. His current research interests include stability theorem and its application research of the differential system, robustness control, neural network, and biomathematics.

Shiping Wen (Senior Member, IEEE) received the MEng. degree in control science and engineering from School of Automation, Wuhan University of Technology, in 2010, and the Ph.D. degree in control science and engineering from the School of Automation, Huazhong University of Science and Technology, in 2013. He is currently a Professor at the Australian Artificial Intelligence Institute (AAII) at University of Technology Sydney. His research interests include memristor-based neural network, deep earning, computer vision, and their applications in medical informatics, etc.

Yuanlun Xie is currently working toward a Ph.D. degree in the School of Information and software engineering, University of Electronic Science and Technology of China. From November 2022 to November 2023, he is currently a visiting researcher with the School of Electrical & Electronic Engineering, Nanyang Technological University, Singapore. His main research interests include the algorithmic theory of machine learning, facial expression recognition by deep learning, and low-light image processing.
All Tables
The maximum acceptable time delay τmax under different preset sampling periods h
All Figures
 |
Figure 1. Networked control systems and application |
| In the text | |
 |
Figure 2. Event-trigger under DoS attacks |
| In the text | |
 |
Figure 3. Schematic diagram of path following model |
| In the text | |
 |
Figure 4. System parameter state trajectory response with DoS attacks |
| In the text | |
 |
Figure 5. System parameter state trajectory response without DoS attacks |
| In the text | |
 |
Figure 6. Release instants and time intervals under GDA |
| In the text | |
 |
Figure 7. Release instants and time intervals under regular algorithm |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


















![$$ \begin{aligned} \alpha (t)&=col\{x(t),x(t_{k}h),x(t_{k+1}h)\},\ \underline{h}_{k}=t_{k+1}h-t_{k},\ \overline{h}_{k}=t-t_{k}h,\ \mathrm{\Pi }_{1}=col\{e_{4}-e_{1}\},\ \mathrm{\Pi }_{2}=col\{e_{1}-e_{3}\},\ \\ \mathrm{\Pi }_{3}&=col\{e_{1},e_{3},e_{4}\},\ \mathrm{\Pi }_{4}=col\{e_{5},\mathbf 0 ,\mathbf 0 \},\ \mathrm{\Phi }=col\left\{ e_{1}-e_{2},e_{1}+e_{2}-2e_{6},e_{1}-e_{2}+6e_{6}-12e_{7}\right\} , \\ \xi (t)&=col\left\{ x(t),x(t-\tau ),x(t_{k}h),x(t_{k+1}h),\dot{x}(t),\frac{1}{\tau }\int ^{t}_{t-\tau }x(s)\,\mathrm{d}s, \right.\\&\quad \left. \frac{1}{\tau ^{2}}\int ^{t}_{t-\tau }\int ^{t}_{u}x(s)\,\mathrm{d}s\,\mathrm{d}u,e\left(t_{k}h\right),e^{dos}\left(t^{+}_{k}h\right),\omega (t)\right\} ,\\ \mathcal {\bar{H}}&=\mathrm{diag} \{\mathcal {H},3\mathcal {H},5\mathcal {H}\},\ e_{i}=\left[0_{n\times (i-1)n}\quad I_{n\times n}\quad 0_{n\times (9-i)}\right],\quad i=1,2,\cdots ,9. \ \end{aligned} $$](/articles/sands/full_html/2023/01/sands20230001/sands20230001-eq27.gif)





![$$ \begin{aligned} \dot{V}_{2}(t)&=\dot{x}(t)\mathcal {M}\left(x\left(t_{k+1}h\right)-x(t)\right)- \left(x(t)-x\left(t_{k}h\right)\right)\mathcal {M}\dot{x}(t)\nonumber \\&\quad +\underline{h}_{k}\alpha ^T(t)\mathcal {Q}\alpha (t) -\overline{h}_{k}\alpha ^T(t)+2\overline{h}_{k}\underline{h}_{k}\alpha ^T(t)\mathcal {Q}\left[\dot{x}(t),\mathbf 0 ,\mathbf 0 \right]^T, \end{aligned} $$](/articles/sands/full_html/2023/01/sands20230001/sands20230001-eq33.gif)

![$$ \begin{aligned}&-\int _{t-\tau }^{t}\dot{x}^T(s)\mathcal {H}\dot{x}(s)\,\mathrm{d}s\le -\left[\begin{matrix}x(t)-x(t-\tau )\\ x(t)+x(t-\tau )-2\int ^{t}_{t-\tau }\frac{x(s)}{\tau }\,\mathrm{d} s\\ x(t)-x(t-\tau )+6\int ^{t}_{t-\tau }\frac{x(s)}{\tau }\,\mathrm{d} s-12\int ^{t}_{t-\tau }\int ^{t}_{u} \frac{x(s)}{\tau ^{2}}\,\mathrm{d}s\,\mathrm{d}u\end{matrix}\right]^T \nonumber \\&\qquad \times \left[ \begin{matrix} {{\mathcal {H}}}&\quad {{0}}&\quad {{0}}\\ {{0}}&\quad {{3\mathcal {H}}}&\quad {{0}}\\ {{0}}&\quad {{0}}&\quad {{5\mathcal {H}}}\\ \end{matrix}\right] \left[\begin{matrix} x(t)-x(t-\tau )\\ x(t)+x(t-\tau )-2\int ^{t}_{t-\tau }\frac{x(s)}{\tau }\,\mathrm{d} s\\ x(t)-x(t-\tau )+6\int ^{t}_{t-\tau }\frac{x(s)}{\tau }\,\mathrm{d} s -12\int ^{t}_{t-\tau }\int ^{t}_{u}\frac{x(s)}{\tau ^{2}}\,\mathrm{d}s\,\mathrm{d}u \end{matrix}\right]. \end{aligned} $$](/articles/sands/full_html/2023/01/sands20230001/sands20230001-eq35.gif)


![$$ \begin{aligned} 0&=2\left[x^T(t)\mathcal {Y}_{1}+\omega ^T(t)\mathcal {Y}_{2}+\dot{x}^T(t)\mathcal {Y}_{3}\right]\left[\mathcal {A}x(t)+\mathcal {B}u(t) +\mathcal {C}\omega (t)-\dot{x}(t)\right]\nonumber \\&=2\left[x^T(t)\mathcal {Y}_{1}+\omega ^T(t)\mathcal {Y}_{2}+\dot{x}^T(t)\mathcal {Y}_{3}\right] \left[\mathcal {A}x(t)+\mathcal {B}\mathcal {K}x\left(t_{kh}\right) +\mathcal {C}\omega (t)-\dot{x}(t)\right]\nonumber \\&=\text{ Sym}\left\{ \xi ^T(t)\mathrm{\Gamma }\mathrm{\Delta }\xi (t)\right\} . \end{aligned} $$](/articles/sands/full_html/2023/01/sands20230001/sands20230001-eq39.gif)







![$$ \begin{aligned} A=\left[\begin{matrix} {{0}}&\quad {{v_{x}}}&\quad {{v_{x}}}&\quad {{0}}\\ [4pt] {{0}}&\quad {{0}}&\quad {{0}}&\quad {{1}}\\ [4pt] {{0}}&\quad {{0}}&\quad {{-\frac{C_{n}+C_{m}}{mv^{2}_{x}}}}&\quad {{-\left(1+\frac{l_{n}C_{n}+l_{m}C_{m}}{mv^{2}_{x}}\right)}}\\ [4pt] {{0}}&\quad {{0}}&\quad {{\frac{l_{n}C_{n}+l_{m}C_{m}}{I_{s}}}}&\quad {{-\frac{l^{2}_{n}C_{n}+l^{2}_{m}C_{m}}{v_{x}I_{s}}}}\\ \end{matrix}\right],\qquad B=\left[\begin{matrix} 0\\ [4pt] 0\\ [4pt] \frac{C_{n}}{mv_{x}}\\ [4pt] \frac{l_{n}C_{n}}{I_{s}}\\ \end{matrix}\right]. \end{aligned} $$](/articles/sands/full_html/2023/01/sands20230001/sands20230001-eq54.gif)