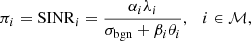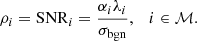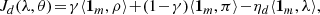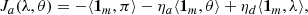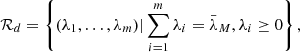1. Problem formulation

1.1. System model and communication channel

Consider a simplified model of a cyber-physical system (CPS) with a physical plant, m wireless sensors, and a remote estimator, which has been widely applied in existing literature [1–3]. It is assumed that there exists a Denial-of-Service (DoS) attacker in the environment. The information CPS states that x_k ∈ ℝ^n_x may be blocked or congested by the attacker at any time. For this reason, the information received by the estimator satisfies

$$\begin{array}{c}\hfill {\widehat{x}}_k^i=\{\begin{array}{cc}{\widehat{x}}_k^{s,i}\hfill & \mathrm{channel}i\mathrm{is\; safe}\mathrm{(without\; DoS\; attack),}\hfill \\ 0\hfill & \mathrm{otherwise,}\hfill \end{array}\end{array}$$(1)

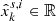where ${\widehat{x}}_k^{s,i}\in \mathbb{R}$ is the value of a certain state at time k. The value is measured by sensor i in real-time. s is the abbreviation of the sensor.

Along with DoS attacks, network transmission is also susceptible to attenuation and interference, which causes data packet dropouts. The signal-to-interference-and-noise ratio (SINR) is introduced as a way to assess the integrity of data after transmission.

$$\begin{array}{c}\hfill {\pi }_i={\mathrm{SINR}}_i=\frac{{\alpha }_i{\lambda }_i}{{\sigma }_{\mathrm{bgn}}+{\beta }_i{\theta }_i},i\in \mathcal{M},\end{array}$$(2)

where ℳ = {1,2,…,m}. m is the number of channels. The fading channel gain of the defender or attacker for the ith channel is denoted by α_i, β_i >  0. The level of background noise is described by σ_bgn. The energy assigned by the defender or attacker to the ith channel is denoted by λ_i, θ_i ≥ 0. If the attacker does not launch DoS attacks, the SINR can be simplified to signal-to-noise ratio (SNR), which is indicated by ρ_i.

$$\begin{array}{c}\hfill {\rho }_i={\mathrm{SNR}}_i=\frac{{\alpha }_i{\lambda }_i}{{\sigma }_{\mathrm{bgn}}},i\in \mathcal{M}.\end{array}$$(3)

1.2. Reward function and strategy

Suppose the probability that there is only background noise in the channel is γ, and both players know the total energy of each other, which are 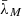${\overline{\lambda }}_M$ and ${\overline{\theta }}_M$. The rewards for the defender and the attacker are given as follows

$$\begin{array}{c}\hfill J_d(\lambda ,\theta )=\gamma ⟨{\mathbf{1}}_m,\rho ⟩+(1-\gamma )⟨{\mathbf{1}}_m,\pi ⟩-{\eta }_d⟨{\mathbf{1}}_m,\lambda ⟩,\end{array}$$(4)

$$\begin{array}{c}\hfill J_a(\lambda ,\theta )=-⟨{\mathbf{1}}_m,\pi ⟩-{\eta }_a⟨{\mathbf{1}}_m,\theta ⟩+{\eta }_d⟨{\mathbf{1}}_m,\lambda ⟩,\end{array}$$(5)

where $\rho ={[{\rho }_1,\dots ,{\rho }_m]}^{\top },\pi ={[{\pi }_1,\dots ,{\pi }_m]}^{\top },\lambda ={[{\lambda }_1,\dots ,{\lambda }_m]}^{\top },\theta ={[{\theta }_1,\dots ,{\theta }_m]}^{\top },{\mathbf{1}}_{\mathbf{m}}={[1,\dots ,1]}_{1\times m}^{\top }$ and η_d, η_a refer to the cost of unit energy consumed by defender and attacker, respectively. ⟨ ⋅ ⟩ denotes the standard inner product in n-dimensional Euclidean space.

The goal of the defender and the attacker is to maximize their reward value. Hence, strategies should be their real-time decisions on energy allocation. The strategy sets ℛ_d, ℛ_a are given for defender and attacker, respectively. 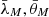${\overline{\lambda }}_M,{\overline{\theta }}_M$ refer to the total energy available for both sides of the game.

$$\begin{array}{c}\hfill {\mathcal{R}}_d=\{({\lambda }_1,\dots ,{\lambda }_m)|\sum _{i=1}^m{\lambda }_i={\overline{\lambda }}_M,{\lambda }_i\ge 0\},\end{array}$$(6)

$$\begin{array}{c}\hfill {\mathcal{R}}_a=\{({\theta }_1,\dots ,{\theta }_m)|\sum _{i=1}^m{\theta }_i={\overline{\theta }}_M,{\theta }_i\ge 0\}.\end{array}$$(7)

2. Main results

In the following contents, theoretical results of Stackelberg equilibrium in static Stackelberg game [5] and strategies for both defender and attacker in dynamic Stackelberg game are given.

2.1. Static game analysis

Given that both sides’ total energy is known, the following optimization problem can be solved to determine the optimal DoS attack strategy for the attacker. Theorem 1 is the theoretical conclusion reached by utilizing the Karush-Kuhn-Tucker (KKT) conditions [6].

$$\begin{array}{c}\hfill \begin{array}{cc}& \underset{\theta \in {\mathcal{R}}_a}{max}-⟨{\mathbf{1}}_m,\pi ⟩\hfill \\ \hfill s.t.& ⟨{\mathbf{1}}_m,\theta ⟩-{\overline{\theta }}_M=0,\hfill \\ \hfill & -{\theta }_i\le 0,i\in \mathcal{M}.\hfill \end{array}\end{array}$$(8)

Theorem 1 Suppose that the defender’s strategy is known as λ. The optimal strategy of energy allocation obtained by the attacker to respond to the defender’s defensive scheme is

$$\begin{array}{c}\hfill {\theta }_i(\lambda )=max\{\frac{1}{{\beta }_i}(\sqrt{\frac{{\alpha }_i\beta i{\lambda }_i}{\overline{\mu }}}-{\sigma }_{\mathrm{bgn}}),0\},i\in \mathcal{M},\end{array}$$(9)

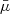where $\overline{\mu }$ is the solution of the following equation

$$\begin{array}{c}\hfill \sum _{i=1}^{M}max\{\frac{1}{{\beta }_i}(\sqrt{\frac{{\alpha }_i{\beta }_i{\lambda }_i}{\overline{\mu }}}-{\sigma }_{\mathrm{bgn}}),0\}={\overline{\theta }}_M.\end{array}$$(10)

Proof. See Appendix A for details.

Meanwhile, a non-convex optimization problem can be solved to determine the defender’s best course of action. The numerical result of Stackelberg Equilibrium is proposed to be found using a self-adaptive particle swarm optimization (PSO). Appendix B contains a complete list of the steps.

Remark 1. The attack-defence model in CPS constructed in this commentary can be extended to the Stackelberg game with multiple attackers and defenders. It has been proved [7, 8] that there exist equilibrium points as long as the reward function of both sides guarantees certain convexity requirements. The procedures of proving the static equilibrium and obtaining the optimal attack strategy are similar [9]. The differences in attack strategy between work [9] and this commentary lie in the physics scene and mathematical modeling. Attackers’ unknown energy is emphasized in work [9], while the probability of launching DoS attacks is considered in this commentary.

2.2. Dynamic game

In mathematical form, the reward function for the defender is undoubtedly a linear function with respect to λ. To express it in vector form, J_d = φ^⊤λ. As a result, the defender can adopt the optimal defensive strategy based on the following theorem.

Theorem 2 Given the attacker’s strategy θ, the optimal response for the defender is to allocate all of its limited energy to the channel with the maximum weight factor φ_i, which is the index of the maximum item in the weight factor vector. If there is not a unique index with the maximum weight factor, then the optimal response for the defender is a set of channels with equal weight factors

$$\begin{array}{c}\hfill \{({\lambda }_{i_1},\cdots ,{\lambda }_{i_k})|{\mathrm{\Sigma }}_{r=1}^k{\lambda }_{i_r}={\overline{\lambda }}_M\}.\end{array}$$(11)

Proof. See Appendix C for details.

Based on Theorem 1 and 2, a computational algorithm can be designed for the evolution of the strategies of both attackers and defenders in a dynamic Stackelberg game.

3. Simulation results

The probability of the attacker’s existence is chosen as γ = 0.4. For simulation, consider the network parameters selected in [3], where m = 4, 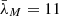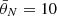${\overline{\lambda }}_M=11$, ${\overline{\theta }}_N=10$, η_a = η_d = 0.3, σ_bgn = 0.2, α = [0.8, 0.7, 0.6, 0.5]^⊤ and β = [0.2, 0.3, 0.4, 0.5]^⊤. The static equilibrium of energy allocation for both the defenders and the attackers is depicted in Figure 1a. In the dynamic game scenario, after 10 000 Monte Carlo simulations, it is found that the energy allocation pattern varies. The reward values are plotted in Figure 1b. Table 1 summarizes the optimal strategies for both defenders and attackers. It is observed that compared to the static equilibrium scenario, even if the amount of energy allocated to each channel and the resulting reward values vary, both defenders and attackers still allocate the majority of their resources to Channel 1 and Channel 2. The additional details of the simulations are included in Appendix E. To further strengthen the novelty of the proposed PSO, a set of comparative experiments is included in the supporting information, as shown in Appendix F.

Figure 1. Reward value of both sides. (a) Self-adaptive PSO. (b) Dynamic game

4. Conclusion

In this commentary, a Stackelberg game framework for a multi-channel CPS consisting of one DoS attacker and one defender is introduced. Simulation results demonstrate that both offline and online strategies demonstrate a tendency to allocate energy to specific channels. In the dynamic game setting, the defender and attacker energy allocation strategies follow a repeating pattern, with the average values approaching static equilibrium levels. Future work will focus on extending the proposed framework to investigate false data injection attacks and replay attacks.

Authors’ Contributions

Zhuping Wang provided the core idea behind this paper. Haoyu Shen was a co-author and driving force behind the creation of this commentary. Hao Zhang provided feedback and corrected errors in the text and was also a co-author. Sheng Gao contributed by verifying theoretical derivations and assisting with simulation experiments. Huaicheng Yan oversaw the completion of the commentary and provided suggestions for future research directions.

Funding

This work is supported by the National Natural Science Foundation of China (62273255, 62088101), Shanghai International Science and Technology Cooperation Project (22510712000, 21550760900), Shanghai Municipal Science and Technology Major Project (2021SHZDZX0100) and Fundamental Research Funds for the Central Universities.

Supporting Information

The supporting information is published as submitted, without typesetting or editing. The responsibility for scientific accuracy and content remains entirely with the authors. Access here

References

© The Author(s) 2024. Published by EDP Sciences and China Science Publishing & Media Ltd.

All Tables

All Figures

	Figure 1. Reward value of both sides. (a) Self-adaptive PSO. (b) Dynamic game
In the text